Tag: SuperCollider

Domifare at Folklore

Even Rascob (aka BITPRINT) has been organising regular Live Code gigs are Folklore in Hackney. I played Domifare last night . . . sort of.

I’ve blogged before about pitch recognition being flaky. And it is, but usually within the first three minutes or so, the SuperCollider autocorrelation UGen does actually recognise the pitches and the piece runs.

Not last night. Instead, I spend 15 minutes playing the same four note phrase over and over and over again, in front of an audience.

What went wrong

  • Normally, when I play this, I have the mic right down in the bell, and it was up slightly higher this time, which may have caused problems.
  • When I practice this, I lip the pitch up or down slightly and this often works. This level of subtlety and control is extremely difficult after several minutes of failure on stage. Instead, my playing got messier and messier over the course of the set.
  • As I was trying to piece out, I couldn’t decide whether to use my old mouth piece, or my new one which is slightly more difficult with greater freedom. It didn’t seem to make a difference when I was practising, so I went for the newer, freer one, which might have been a mistake.
  • My sound card’s output was also extremely low, which is a problem I’ve had before with Pipe Wire. This was concerning during the tech setup, but turned out not to be an issue during the performance.
  • My laptop was sat on a stool in front of me which was not a distance that worked at all with my glasses. The screen was so blurry, I couldn’t properly tell what notes were arriving.

How to fix it

  • If I need consistent mic placement that’s down in the bell, I should make a mount that goes into the bell. The would be a cork-covered ring, with spokes, a mic suspended in the middle.
  • Flucoma would allow me to train a neural net to recognise a series of pitches as a cue. Because the tuba spectrum is weird and the mic is most sensitive at the weird points, I would probably have to do the training on stage. Would his be more tedious of 15minutes of failed command input? No.
  • Practising this piece is essentially training myself to be decipherable to the algorithm, which is subtly different than normal practice goals or technique. I did not get as much practice as I would have liked. I spent a lot of time building lip strength, with the idea it would make my notes clearer, but not as much time getting feedback from the autocorrelation algorithm. It may be more practice with the program would have helped. Or, the algorithm was confused by background noise or mic placement, perhaps it would have made no difference whatsoever.
  • Taking the bus with a tuba, a laptop, an audio card, cables, a mic, a mic stand and so forth is already a bit much, but it may be the case that I also need a laptop stand so I can ensure my computer being at a height and location where I can see it. Or my old reading glasses required more and more distance. Maybe a laptop on a stool is not a good use for them.

How I dealt with everything

I think my stage presence was fine, actually, except for when I was giving up at the end. I should have launched a few minutes of solo improv starting from and around the cue phrase. I’m going to practice this a bit, not that I expect the piece to fail like this again.

This was not my first performance of this piece. It went fine when I played it in Austria, 3 years ago.

Well, at least the failure of that piece was all that went wrong

Shelly Knotts and I were also meant to play some MOO, but discovered during the sound check that most of it wasn’t working, so we cut it from the programme.

Audience Reactions

People were generally positive. Multiple people used the word “futility” but with a positive intention. Which goes to show you can’t trust nerds.

To do

  • Incorporate Flucoma
  • Play this on Serpent because it’s more portable and I really do have more freedom of pitch.
Video by Shelly Knotts

Domifare GUI improvements

A SuperCollider GUI window with buttons across the top, a server meter, a large text area, a list tot he side, an input bar, a bass cleff with nothing following it, four sliders controlling thresholds, two images containing four bass cleff cyctems between them, labelled, "Record Loop", "Stop" "Shake" and "Unshake"
The GUI for Domifare

Domifare is back under development because I will be performing with it on Monday evening in London, at Folklore. https://lu.ma/2rkkzmcz

All the improvements thus far have been to the GUI. It’s come a long way, but there are still some persistent bugs: you must resize the window to get the GUI to layout correctly. The new SuperCollider sclang version is a release candidate right now, so I’m holding off fixing everything, as I hope the many conflicting GUI methods will be better harmonised in that version.

The project is relying on BiLETools for several of the widgets because I was having problems with EZSliders. Again, after the major version update, I plan to remove this dependency.

The Key class in TuningLib is no longer required. It was always overkill, and some of it’s functionality has broken in the last three years.

In general, the pitch tracking is working better than it did three years ago, especially the autocorrelation, although there is still a high error rate. The built in “cheat sheet” makes this much easier to use, although I fear it lets the audience in a bit too much on how simplistic this whole setup is.

The notation is all generated via MuseScore, saved as SVG and then edited in Inkscape. The version of SC on my computer won’t open SVG files (or at least not inkscape SVGs), so these are exported to PNG. The lone F clef in the middle of the image adds notes to the right as it recognises them. The language parser does not track octaves, so it displays noteheads inside the lower part of the staff.

Adding the octave tracking is only partially fiddly, but doing this properly would entail turning the new class CleffView into a proper notation layout class. That has obvious utility, but its ore geometry than I want to get into right now.

I may upgrade the variable list from being a BtListView / EZListView to being a stack of ObjectGUIs for the DomifareLoop class. This would be valuable because I could indicate whether they were playing or were shaken. This could also include their name spelled via CleffViews. Or I could just learn to play directly from solfedge.

Another possible future improvement could be the inclusion of Solresol character glyphs, which would have a fun alien vibe. The problems are both that (last I looked) there is not a nice Linux font that supports these and it would require a time investment to be able to play variables names listed that way.

I’ve also misspelled “clef” as “cleff” but a find and replace is giving me crash errors, so idk. Shrug. Sad face. You can see the latest version on GitHub, although this will move to Codeberg hopefully soon.

There’s a very obvious case for integrating Flucoma into this project to recognise gestures. This would also entail building a training interface. The informational webpage for the SuperCollider release candidate specifically mentions that Flucoma does not work with it, so this is also deferred until that gets fixed. I don’t want to have to hold off upgrading SuperCollider, so I cannot create a situation where upgrading breaks this project.

Some of the London live coders (Lu) have expressed enthusiasm for the idea of doing the training as part of the performance. That has president for cybernetic pieces like Hornpipe by Gordon Mumma and remains a very good idea, but still not for Monday.

If this sounds cool and you can’t come on Monday, maybe you could let me know of another gigging opportunity in your town that I could play at? I’d like to take this show on the road!

Navigating ScMoo

In my previous post, I described how to install and start the SuperCollider Moo. In this post, I’m going to talk about how to use and move around the Moo.

Note this is an early version and it’s my intention to gradually make the SC Moo align more closely with LambdaMOO commands and syntax. Note also that the database is static. Your changes will be visible to yourself and others while you are logged in, but they will not be saved. If you make something you really like, please keep a local copy of it.

When you log in, you’ll see a lot of messages in the SC Post window, including loads of error messages. Just hold on until the GUI opens. This GUI will have a random colour, but it will have three text areas.

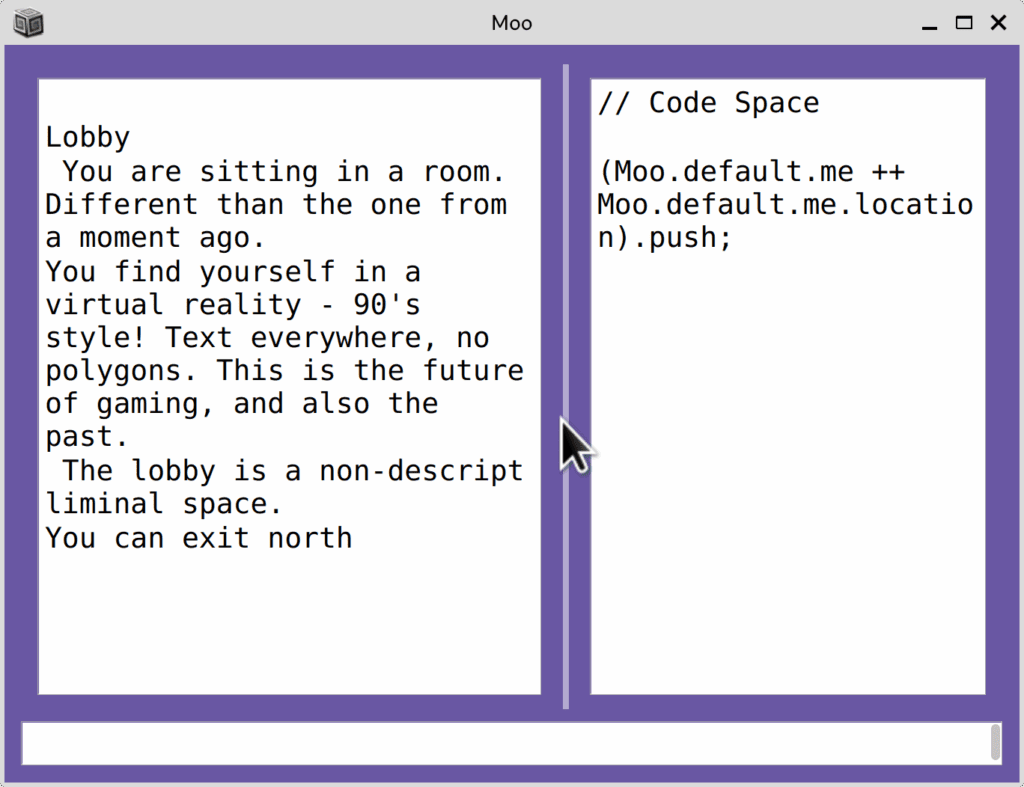
The Moo's GUI. The mouse is clicking and dragging on the gray line between the two panes to change the relative sizes.
The Moo GUI

The left hand side is the Moo’s output. The right hand side and bottom are both input. The right hand side is designed to enable entering code. If you just want to use the Moo as a user, you can make that side smaller by clicking and dragging on the grey line that separates the two sides. Then just enter your Moo commands in the bottom text area, followed by enter or return to evaluate them.

When you log in, your character will connect to the lobby. You will see text describing the room. Below that, you will see a list of objects if any are present. Below that, a list of other users, if any are present. And finally, a list of exits. If there are not exits, it will say “There is no way out” because I thought that was funny.

You can look again at the room any time by tying “look” (without the quotes) and pressing enter in the bottom text area of the window. In the current iteration of the database, the lobby contains a flyer. To look at it, you can type “look flyer” and hit enter. To look at yourself, type “look me“.

The default message for what you look like isn’t very exciting, so you might take a moment to change it. Type ‘ describe me as "My description goes here." ‘ (without the single quotes). Put your description inside double quotes. After you change it, try look me again. This is what others will see when they look at your character.

You can move through the Moo by typing the names of the exits. From the lobby, you can type “north“. This will place you in the bar, which has several objects. You can look at all of them and some of them have additional verbs – that is they are interactive. To see the verbs on an object type “verbs ” followed by the name of the object. For example, “verbs cage” will tell you the verbs on the cage. From that, you’ll see that one of the verbs is climb, so try climb cage.

Some of the verbs have audio on them and some don’t. Some of the objects have attached sound and some don’t. Let’s look at the jukebox. The verbs on it aren’t promising. We can’t describe it because we’re not the owner and it doesn’t seem to have anything in about playing it. So let’s put our own audio on it.

Go to the right hand side of GUI and evaluate the SuperCollider code (Moo.default.me ++ Moo.default.me.location).push; Now we can live code the jukebox, which has been added to the environment as ~jukebox.

We can set a pattern ~jukebox.pattern = Pbind(); and then play it ~jukebox.play; The resulting pattern is super boring, so why not modify it? ~jukebox.pattern = Pbind(\freq, 330); You can then live code it as you would with Pbinds or any other kind of pattern. You can set any SynthDef you’d like. As of now, all of these interventions are entirely local, alas, but networking them is coming.

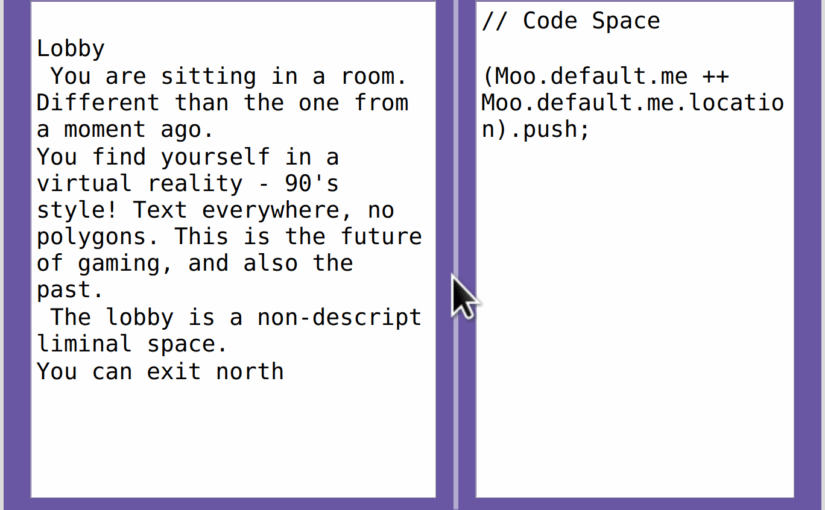
Logging in to SCMoo

Friends, I wrote a Moo in SuperCollider.

Well, it’s partially written. Anyway, the point is that you can log in and play with the database developed by Shelly Knotts.

A proper tutorial will be coming, but between this, the included help files and the Github Readme should be enough to get started. If you experience any problems with this script, please leave a comment or reply.

Before you run it the first time, you must install two Quarks.

Quarks.install("https://github.com/celesteh/BiLETools.git");
Quarks.install("https://github.com/celesteh/SCMoo.git");

This should cause the required Quark, JSONlib, to automatically install.

Then you will need to run all of the following code, which you may wish to save in an scd file. Please edit it so variable a gets your name. 


(
a = "MyName";
g = "Moo".toUpper;

w = MooWebSocketResponder(a,"UserPassword",g,"GroupPassword", "https://moo.blessing.exchange/osc.html").echo_(true);

s.waitForBoot({

	//trapdoor

	SynthDef(\trapdoorCrash, {|out, amp=02, gate=1, pan=0, dur=1|

		var env, noise, chaos, panner, sin, senv, sline, sfreq;

		chaos = EnvGen.kr(Env.perc) * 2;
		noise = Crackle.ar(chaos, amp);
		senv =  EnvGen.kr(Env.perc) * 200;
		sfreq = Rand(60, 80);
		sline = XLine.kr(sfreq, 50, 1);
		sin = SinOsc.ar(sline + senv) / 2;
		env = EnvGen.kr(Env.perc, doneAction:2);
		panner = Pan2.ar(noise + sin, pan, env);
		Out.ar(out, panner);
	}).add;



	// 7 midi
	SynthDef(\trapdoorSines, {|midinote, amp, dur, gate=1, out|
		var sines, env, filter;

		env = EnvGen.kr(Env.asr, gate, doneAction:2);
		sines = Splay.ar(
			[0.5, 1, 2, 4].collect({|i|
				[
					SinOsc.ar(((midinote - 7).midicps *i), 0, amp),
					SinOsc.ar(((midinote).midicps *i), 0, amp),
					SinOsc.ar(((midinote + 7).midicps *i), 0, amp)
				]
		}).flat, 1, env);
		filter = BBandPass.ar(sines, 500);
		Out.ar(out, filter);
	}).add;

	SynthDef(\trapdoorOpen, {|out, amp=02, gate=1, dur=1|
		var pos, saw, env, freq, panner;

		pos = SinOsc.ar(2/dur);
		freq = (pos * 150) + 150;
		saw = Saw.ar(freq, amp);
		env = EnvGen.kr(Env.asr, gate, doneAction:2);
		panner = Pan2.ar(saw, pos, env);

		Out.ar(out, panner);
	}).add;

	SynthDef(\trapdoorSplash, {|out, amp=02, gate=1, dur=1, pan=0|

		var noise, panner, env, fenv, filter;

		noise = WhiteNoise.ar(amp*2);
		fenv = (EnvGen.kr(Env.perc(releaseTime:dur)) * 400) + XLine.kr(800, 200, dur);
		filter = RLPF.ar(noise, fenv);
		env = EnvGen.kr(Env.adsr, gate, doneAction:2);
		panner = Pan2.ar(filter, pan, env);

		Out.ar(out, panner);
	}).add;


	// bats

	SynthDef(\batAttack, {|freq, amp, dur, gate=1, pan, out|

		var sin, panner, env, pmenv, pm;

		pmenv = (EnvGen.kr(Env.adsr) * pi) + (pi/3);
		pm= SinOsc.ar(freq * (37/41), 0, pmenv);
		sin = SinOsc.ar(freq, pm, amp);
		env = EnvGen.kr(Env.adsr, gate, doneAction:2);
		panner = Pan2.ar(sin, pan, env);
		Out.ar(out, panner);
	}).add;

	SynthDef(\batSing, {|freq, amp, dur, gate=1, pan, out|

		var trig, vosim, panner, filter, env;

		trig = Impulse.ar(freq/2, 0.1, EnvGen.kr(Env.asr, gate));
		vosim = VOSIM.ar(trig, freq*3);
		filter = BPF.ar(vosim, freq*2);
		env = EnvGen.kr(Env.triangle(dur), doneAction:2);
		panner = Pan2.ar(filter, pan, env);
		Out.ar(out, panner)
	}).add;

	SynthDef(\batPing, {|freq, amp, dur, gate=1, pan, out|

		var sin, env, panner;

		sin = SinOsc.ar(freq, 0, amp*2);
		env = EnvGen.kr(Env.perc, doneAction:2);
		panner = Pan2.ar(sin, pan, env);
		Out.ar(out, panner);
	}).add;

	SynthDef(\bass, { |out=0,amp=0.1,sustain=0.2,freq=200,fb=0, room=3, mix=0.5, res=0, nois=0.2, trem_freq=4, depth=0.9, rel=0.1, att=0.01, frange=50, del=0.05, comb=0.2, freq_n=3, width=1.0, dec=0.01|
		var snd, env, ctrl;

		//ctrl = ;
		snd = Saw.ar([freq, freq+10], 1).tanh; // * LFNoise1.kr(trem_freq).range(depth, 1);
		snd = snd + Pulse.ar(freq*0.5, 0.6).dup;
		snd = snd + Pluck.ar(WhiteNoise.ar(1), 1, freq.reciprocal, freq.reciprocal, 10, 0);
		// SinOscFB.ar([freq, freq + 10], fb,1).tanh * LFNoise1.kr(trem_freq).range(depth, 1);
		// snd = snd + BrownNoise.ar(nois).tanh;
		// snd = snd * (Crackle.ar(LFNoise1.kr(3).range(1.0, 2.0)) * 0.3).tanh;
		snd = RLPF.ar(snd, freq + 100, 0.8);
		snd = FreeVerb.ar(snd, mix, room).tanh;
		// snd = DFM1.ar(snd, freq, res);
		env = EnvGen.ar(Env.perc(att,rel),doneAction:2);
		// env = EnvGen.ar(Env.linen(att,sustain, rel),doneAction:2);
		OffsetOut.ar(out, snd.dup * env * amp);
	}).add;

	SynthDef(\whale, { |out=0,amp=0.1,sustain=0.01,freq=200,fb=0, room=15, mix=0.8, res=0, nois=0.5, trem_freq=4, depth=0.9, rel=0.5, att=0.1, frange=50, del=0.05, comb=10, freq_n=3|
		var snd, env, ctrl;

		//ctrl = ;
		// snd = Formants.ar(LFNoise1.kr([freq_n, freq_n+1, freq_n-1, freq_n+2]).range(freq, freq+frange) * [1, 1.1, 1.2, 1.3], Vowel([\e, \o, \u], [\alto, \tenor])) * 3; // * LFNoise1.kr(trem_freq).range(depth, 1);

		snd = Splay.ar(SinOscFB.ar([freq, freq + 10, freq + 20, freq + 30], fb,1).tanh);
		snd = Splay.ar(PitchShift.ar(snd, 0.2, LFNoise1.kr(0.2).range(1, Array.fill(4, { rrand(0.5, 0.2)} )))).tanh;
		snd = DelayC.ar(RLPF.ar(snd, Rand(100, 3000), 0.03), 1, 1 / (2), 1, snd * 0.5);
		// snd = BrownNoise.ar(nois).tanh;
		// snd = snd * (Crackle.ar(LFNoise1.kr(0.7).range(1.0, 2.0)) * 0.3).tanh;
		// snd = snd * (PinkNoise.ar(LFNoise1.kr(0.3).range(1.0, 2.0)) * 0.3).tanh;
		// snd = CombC.ar(snd, 0.1, LFNoise1.kr(comb).range(0.03, 0.1));
		snd = FreeVerb.ar(snd, mix, room).tanh;
		// snd = DFM1.ar(snd, freq, res);
		env = EnvGen.ar(Env.linen(att,sustain, rel),doneAction:2);
		OffsetOut.ar(out, snd.dup * env * amp);
	}).add;

	SynthDef(\lake_eels, { |out=0,amp=0.1,sustain=0.01,freq=200,fb=0, room=3, mix=0.5, res=0, nois=0.2, trem_freq=4, depth=0.9, rel=0.5, att=0.1, frange=50, del=0.05, comb=0.3, freq_n=3|
		var snd, env, ctrl;

		//ctrl = ;
		snd = SinOsc.ar([440, 442] * SinOsc.ar(LFTri.kr(0.5).range(5, 50), 0, LFTri.kr(0.4).range(5, 50)), 0, 1); // * LFNoise1.kr(trem_freq).range(depth, 1);

		// SinOscFB.ar([freq, freq + 10], fb,1).tanh * LFNoise1.kr(trem_freq).range(depth, 1);
		snd = snd + BrownNoise.ar(nois).tanh;
		// snd = snd * (Crackle.ar(LFNoise1.kr(3).range(1.0, 2.0)) * 0.3).tanh;
		snd = CombC.ar(snd, 0.1, LFNoise1.kr(comb).range(0.03, 0.1));
		snd = RLPF.ar(snd, LFSaw.kr(0.3).range(2000, 500));
		snd = Mix.ar(FreeVerb.ar(snd, mix, room)).tanh;
		snd = Pan2.ar(snd, SinOsc.ar(LFTri.kr(0.1).range(1, 3)).range(-1, 1));
		// snd = DFM1.ar(snd, freq, res);
		env = EnvGen.ar(Env.linen(att,sustain, rel),doneAction:2);
		OffsetOut.ar(out, snd * env * amp);
	}).add;

	\Formants.asClass.notNil.if({
		"""
SynthDef(\witch, { |out=0,amp=0.1,sustain=0.01,freq=200,fb=0, room=3, mix=0.5, res=0, nois=0.2, trem_freq=4, depth=0.9, rel=0.5, att=0.1, frange=50, del=0.05, comb=10, freq_n=3, mult=1|
var snd, env, ctrl;

//ctrl = ;
snd = Formants.ar(LFNoise1.kr([freq_n, freq_n+1, freq_n-1, freq_n+2]).range(freq, freq+frange) * mult, Vowel([\e, \o, \u], [\alto, \soprano])) * 3; // * LFNoise1.kr(trem_freq).range(depth, 1);
snd = snd + SinOsc.ar([freq, freq*1.05] * SinOsc.ar(LFSaw.kr(0.5).range(50, 20), 0, LFSaw.kr(0.4).range(20, 50)), 0, 1);

// SinOscFB.ar([freq, freq + 10], fb,1).tanh * LFNoise1.kr(trem_freq).range(depth, 1);
// snd = snd + BrownNoise.ar(nois).tanh;
// snd = snd * (Crackle.ar(LFNoise1.kr(3).range(1.0, 2.0)) * 0.3).tanh;
// snd = CombC.ar(snd, 0.1, LFSaw.kr(comb).range(0.05, 0.01));
snd = FreeVerb.ar(snd, mix, room).tanh;
// snd = DFM1.ar(snd, freq, res);
env = EnvGen.ar(Env.linen(att,sustain, rel),doneAction:2);
OffsetOut.ar(out, snd.dup * env * amp);
}).add;
""".interpret;
	});


	SynthDef(\spider, { |out=0,amp=0.1,sustain=0.01,freq=200,fb=0, room=3, mix=0.5, res=0, nois=0.2, trem_freq=4, depth=0.9, rel=0.5, att=0.1, frange=50, del=0.05, comb=0.2, freq_n=3, width=1.0|
		var snd, env, ctrl;

		//ctrl = ;
		snd = Pulse.ar([freq, freq+10], LFTri.kr(1).range(0, width), 1).tanh; // * LFNoise1.kr(trem_freq).range(depth, 1);

		// SinOscFB.ar([freq, freq + 10], fb,1).tanh * LFNoise1.kr(trem_freq).range(depth, 1);
		// snd = snd + BrownNoise.ar(nois).tanh;
		// snd = snd * (Crackle.ar(LFNoise1.kr(3).range(1.0, 2.0)) * 0.3).tanh;
		snd = CombC.ar(snd, 0.1, LFNoise1.kr(comb).range(0.03, 0.1));
		snd = FreeVerb.ar(snd, mix, room).tanh;
		// snd = DFM1.ar(snd, freq, res);
		env = EnvGen.ar(Env.perc(att,sustain),doneAction:2);
		// env = EnvGen.ar(Env.linen(att,sustain, rel),doneAction:2);
		OffsetOut.ar(out, snd.dup * env * amp);
	}).add;


	\Formants.asClass.notNil.if({

		"""
SynthDef(\ghosts, { |out=0,amp=0.1,sustain=0.01,freq=200,fb=0, room=3, mix=0.5, res=0, nois=0.2, trem_freq=4, depth=0.9, rel=0.5, att=0.1, frange=50, del=0.05, comb=10, freq_n=3, cfreq=3|
var snd, env, ctrl;

//ctrl = ;
snd = Formants.ar(LFNoise1.kr([freq_n, freq_n+1, freq_n-1, freq_n+2]).range(freq, freq+frange) * [1, 1.1, 1.2, 1.3], Vowel([\e, \o, \u], [\alto, \tenor])) * 3; // * LFNoise1.kr(trem_freq).range(depth, 1);

// SinOscFB.ar([freq, freq + 10], fb,1).tanh * LFNoise1.kr(trem_freq).range(depth, 1);
snd = snd + BrownNoise.ar(nois).tanh;
snd = snd * (Crackle.ar(LFNoise1.kr(cfreq).range(1.0, 2.0)) * 0.3).tanh;
snd = CombC.ar(snd, 0.1, LFNoise1.kr(comb).range(0.03, 0.1));
snd = FreeVerb.ar(snd, mix, room).tanh;
// snd = DFM1.ar(snd, freq, res);
env = EnvGen.ar(Env.linen(att,sustain, rel),doneAction:2);
OffsetOut.ar(out, snd.dup * env * amp);
}).add;
""".interpret;
	});


	SynthDef(\dog, { |out=0,amp=0.1,sustain=0.01,freq=440,fb=0, room=3, mix=0.5, res=0, nois=0.5, trem_freq=4, depth=0.8, rel=0.5, att=0.1|
		var snd, env, ctrl;

		//ctrl = ;
		snd = SinOscFB.ar([freq, freq + 10], fb,1).tanh * LFNoise1.kr(trem_freq).range(depth, 1);
		// snd = snd + BrownNoise.ar(nois).tanh;
		// snd = snd * (Crackle.ar(LFNoise1.kr(3).range(1.0, 2.0)) * 4).tanh;
		snd = FreeVerb.ar(snd, mix, room).tanh;
		// snd = DFM1.ar(snd, freq, res);
		env = EnvGen.ar(Env.linen(att,sustain, rel),doneAction:2);
		OffsetOut.ar(out, snd.dup * env * amp);
	}).add;

	SynthDef(\bar1, {|out=0,amp=0.1,sustain=0.01,freq=440,fb=0, room=3, mix=0.5, res=0.99, nois=0.5, trem_freq=4, depth=0.8, rel=0.5, att=0.1|
		var snd, env, ctrl;

		//ctrl = ;
		snd = SinOscFB.ar([freq, freq], fb, 1).tanh;
		// snd = snd + BrownNoise.ar(nois).tanh;
		// snd = snd * (Crackle.ar(LFNoise1.kr(3).range(1.0, 2.0)) * 4).tanh;
		snd = FreeVerb.ar(snd, mix, room).tanh;
		// snd = DFM1.ar(snd, freq, res);
		env = EnvGen.ar(Env.perc(att,sustain),doneAction:2);
		OffsetOut.ar(out, snd.dup * env * amp);
	}).add;

	SynthDef(\mocktail, { |out=0,amp=0.1,sustain=0.01,freq=440,fb=0, room=3, mix=0.5, res=0.99, nois=0.5, trem_freq=4, depth=0.8, rel=0.5, att=0.1|
		var snd, env, ctrl;

		//ctrl = ;
		snd = SinOscFB.ar([freq], fb,1).tanh * LFNoise1.kr(trem_freq).range(depth, 1);
		// snd = snd + BrownNoise.ar(nois).tanh;
		snd = snd * (Crackle.ar(LFNoise1.kr(3).range(1.0, 2.0)) * 4).tanh;
		snd = snd + Dust.ar(10);
		// snd = Decay2.ar(snd, 0.01, 0.1, WhiteNoise.ar);
		snd = DelayN.ar(snd, 0.2, 0.2, 1, snd);
		// snd = DFM1.ar(snd, freq, res);
		snd = snd * (Crackle.ar(LFNoise1.kr(10).range(1.0, 2.0)) * 4).tanh;
		snd = FreeVerb.ar(snd, mix, room).tanh;
		// snd = DFM1.ar(snd, freq, res);
		env = EnvGen.ar(Env.linen(att,sustain, rel),doneAction:2);
		OffsetOut.ar(out, snd.dup * env * amp);
	}).add;

	SynthDef(\cage, {|out=0,amp=0.1,sustain=0.01,freq=440,fb=0, room=3, mix=0.5, res=0.99, nois=0.5, trem_freq=4, depth=0.8, rel=0.5, att=0.1|
		var snd, env, ctrl;

		//ctrl = ;
		snd = SinOscFB.ar([freq, freq], fb, 1).tanh;
		// snd = snd + BrownNoise.ar(nois).tanh;
		// snd = snd * (Crackle.ar(LFNoise1.kr(3).range(1.0, 2.0)) * 4).tanh;
		snd = FreeVerb.ar(snd, mix, room).tanh;
		// snd = DFM1.ar(snd, freq, res);
		env = EnvGen.ar(Env.perc(att,sustain),doneAction:2);
		OffsetOut.ar(out, snd.dup * env * amp);
	}).add;


	\Formants.asClass.notNil.if({
		"""
SynthDef(\barperson, { |out=0,amp=0.1,sustain=0.01,freq=200,fb=0, room=3, mix=0.5, res=0, nois=0.5, trem_freq=4, depth=0.9, rel=0.5, att=0.1, frange=50, del=0.08|
var snd, env, ctrl;

//ctrl = ;
snd = Formants.ar(LFNoise1.kr(5).range(freq, freq+frange), Vowel([\e, \o], [\alto, \tenor])) * 2 * LFNoise1.kr(trem_freq).range(depth, 1);

// SinOscFB.ar([freq, freq + 10], fb,1).tanh * LFNoise1.kr(trem_freq).range(depth, 1);
// snd = snd + BrownNoise.ar(nois).tanh;
snd = snd * (Crackle.ar(LFNoise1.kr(3).range(1.0, 2.0)) * 0.3).tanh;
snd = CombC.ar(snd, 0.1, del);
snd = FreeVerb.ar(snd, mix, room).tanh;
// snd = DFM1.ar(snd, freq, res);
env = EnvGen.ar(Env.linen(att,sustain, rel),doneAction:2);
OffsetOut.ar(out, snd.dup * env * amp);
}).add;
""".interpret;
	});


	s.sync;

	//w.getJSON({|json| json.debug("command line"); j = json; "JSON retrieved".postln});

	AppClock.sched(0, {
		w.getJSON({|json| json.debug("command line");

			AppClock.sched(0.5, {
				n = NetAPI.other(a, g, path:w);

				{
					4.wait;
					m = Moo.login(n, json, \parseText, rest:0.03);
					AppClock.sched(1, {
						m.gui.fontSize = 14;
						{
							var spider, ghosts, witch, lake, barperson, cage, mocktail, dog;

							spider = m[5929];
							ghosts = m[7668];
							witch = m[6360];
							lake = m[8829];
							barperson = m[6832];
							cage = m[5746];
							mocktail = m[4203];
							dog = m[3486];

							barperson.stop;
							barperson.pattern_(Pbind(\instrument, \barperson,
								\dur, barperson[\dur],
								\degree, Prand([1, 4, 2], 5) * (((Pfunc({barperson[\degree].value}) + 1)).round(1)),
								// \legato, 0.001,
								\scale, Scale.minor,
								\att, barperson[\att],
								\rel,  barperson[\rel],
								\room, 0.5,
								\octave, Prand([5, 4], inf),
							));

							cage.stop;
							cage.pattern_(Pbind(\instrument, \cage,
								\dur, Pfunc({cage[\dur].value}) * Pstutter(8, Pseq([1, 0.8, 0.6],inf), inf),
								\degree, (Pseq([0, 1, 2, 3, 4], 5) + Pstutter(5, Pseq([0, 3, 6, 9],inf), inf)) + (((Pfunc({ cage[\degree].value}) + 1)).round(1)),
								// \legato, 0.001,
								\scale, Scale.minor,
								\att, cage[\att],
								\rel, cage[\rel],
								\fb, cage[\fb],
								\room, cage[\room],
								\octave, Pstutter(4, Pseq([5, 6, 7], inf), inf),
							));

							mocktail.stop;
							mocktail.pattern_(Pbind(\instrument, \mocktail,
								\dur, mocktail[\dur],
								\degree, Pseq([1, 2, 7, 5, 2, 4], 25) * (((Pfunc({ mocktail[\degree].value}) + 1)).round(1)),
								// \legato, 0.001,
								\scale, Scale.minor,
								\att, mocktail[\att],
								\rel, mocktail[\rel],
								\fb, mocktail[\fb],
								\room, 0.5,
								\octave, Pstutter(4, Pseq([6, 5, 4], inf), inf),
							));

							dog.stop;
							dog.pattern_(Pbind(\instrument, \dog,
								\dur, dog[\dur],
								\degree, Pseq([1, 4, 2], 2) * (((Pfunc({dog[\degree].value}) + 1)).round(1)),
								// \legato, 0.001,
								\scale, Scale.minor,
								\att, dog[\att],
								\rel,  dog[\rel],
								\fb, dog[\fb],
								\room, 0.5,
								\octave, Pstutter(3, Pseq([5, 4], inf), inf),
							));


							spider.stop;
							spider.pattern_(Pbind(\instrument, \spider,
								\dur, spider[\dur],
								\degree, Pseq((0..8), 3) + Pstutter(5, Pseq([2, 4, 6, 8], inf), inf) + (((Pfunc({~spider[\degree].value}) + 1)).round(1)),
								// \legato, 0.001,
								\scale, Scale.minor,
								\freq_n, spider[\freq_n],
								\att, spider[\att],
								\rel,  spider[\rel],
								\fb, spider[\fb],
								\room, spider[\room],
								\octave, spider[\oct],
							));


							ghosts.stop;
							ghosts.pattern_(Pbind(\instrument, \ghosts,
								\dur, ghosts[\dur],
								\degree, Pseq([1], 1) * (((Pfunc({ghosts[\degree].value}) + 1)).round(1)),
								// \legato, 0.001,
								\scale, Scale.minor,
								\freq_n, ghosts[\freq_n],
								\att, ghosts[\att],
								\rel,  ghosts[\rel],
								\nois, ghosts[\nois],
								\fb, ghosts[\fb],
								\room, ghosts[\room],
								\cfreq, ghosts[\cfreq],
								\frange, ghosts[\frange],
								\comb, ghosts[\comb],
								\octave, ghosts[\oct], //Pseq([4], inf),
							));


							witch.stop;
							witch.pattern_(Pbind(\instrument, \witch,
								\dur, witch[\dur],
								\degree, (Pseq([5, 4, 3, 2, 1], 2) + Pstutter(5, Pseq([0, -1], inf), inf))* (((Pfunc({~witch[\degree].value}) + 1)).round(1)),
								// \legato, 0.001,
								\scale, Scale.minor,
								\freq_n, witch[\freq_n],
								\att, witch[\att],
								\rel,  witch[\rel],
								\sustain, 0.5,
								\fb, witch[\fb],
								\room, 0.5,
								\octave, Pseq([4], inf),
							));

							lake.stop;
							lake.pattern_(Pbind(\instrument, \lake_eels,
								\dur, lake[\dur],
								\degree, Pseq([1], 2) * (((Pfunc({lake[\degree].value}) + 1)).round(1)),
								// \legato, 0.001,
								\scale, Scale.minor,
								\freq_n, lake[\freq_n],
								\att, lake[\att],
								\rel,  lake[\rel],
								\fb, lake[\fb],
								\room, 0.5,
								\octave, Pseq([4], inf),
							));



						}.fork;
					}, nil);

				}.fork

			}, nil);

		});
	}, nil)

});


)


//n = NetAPI.other(a, g, path:w, joinAction:{"Join the Moo now".postln});
//m = Moo.login(n, j, \parseText);

Octatonic Scales in SuperCollider

You can generate your own Octatonic scale in an arbitrary Equal Temperament using the following code.

Change octaveRatio to the ratio you’d like and steps to the number of steps. The Scale is saved to the global variable o;

(

var octaveRatio = 2, steps = 12;
var ratio, tuning_arr, tuning, octatonic_arr, octatonicScale, index;

ratio = octaveRatio.pow(steps.reciprocal);

tuning_arr = steps.collect({|i| ratio.pow(i).ratiomidi });
tuning = Tuning(tuning_arr, octaveRatio);

index = 0;
octatonic_arr =[];

{index < steps }.while({
	octatonic_arr = octatonic_arr.add(index);
	index = index+2;
	(index <= steps).if({
		octatonic_arr = octatonic_arr.add(index);
	});
	index = index + 1;
});


octatonicScale = Scale(octatonic_arr, tuning: tuning);

o = octatonicScale;
)

You can then use this in a Pbind by using \scale. For example:

(
Pbind(
	\scale, o,
	\degree, Prand((0..7), 7)
).play
)

It works!

After many very long days, My project Domifare is working. For me. It won’t work for you because there is a bug in TuningLib. I have raised an issue, which the package maintainer will get to shortly. The package maintainer, who is me will fix it shortly. When I get back from Austria. I need to test my fix properly.

Only a subset of specified commands have been implemented, but I can record a loop and re-order the playback of a loop based on detected onsets. Hypothetically, I can also start and stop loops. In practice, pitch detection is terrible and the language is barely usable. Annoyingly, the utility of it depends on how good my tuba playing sounds.

If I want to use this as an actual tool, the way forward is playing the key phrases in as training data to an AI thing.

While writing this project, I raised three issues with the SuperCollider project over documentation and one issue with the LinuxExternals Quark over Pipewire. That will turn into a merge request. I might update the documentation for it.

If you want to hear this thing in progress, I’ll be using it on Friday. You can turn up in person to Linz, Austria or tune into the live stream. This is part of AMRO, who have a helpful schedule.

I feel like a zombie and will say something more coherent later.

Midosoldo

I put in a bid to play Domifare at AMRO, knowing it was in no state to perform, but also knowing that nothing motivates like a deadline. I thought it was likely to be accepted, so I planned to start working on it during the break between spring and summer terms.

But then I got covid and felt terrible for weeks, but also got brain fog which, to be honest, has not completely dissipated. I mean, it’s hard to tell. How could I possibly have a bassline on my mental state? I do know that my sense of taste is still messed up and if I exercise a lot I feel ill the next day, so let’s say I’m not at 100% mentally. It could be all in my head, but what difference would that make?

I wanted to finish my marking before dedicating all my time to this. I have not finished my marking, but now both are an emergency. Indeed, the list of things I have not done is kilometres long. My tuba needs a service. I haven’t played it for months and lips are completely unfit.

This is an overly-honest research update. The subject line is the Solresol word for “fear.”

This is the state of the language:

Domifare Notes
Domifare Performance Notes

The “language” has always been conceived of as a way of defining loops. So I have some syntax for recording loops as an audio recording or as a series of onsets, the ability to “shake” an onset loop, the ability to schedule shakes, and the ability to start and stop loops. These are all a series of short musical licks I should ideally memorise but at least be able to play without hesitation or split notes.

Meanwhile, the language currently has the ability to read and receive notes, which is necessarily flaky and a scaffold to hand the rest of the operations …. and a GUI to adjust thresholds because that’s necessary while playing… and that’s kind of it.

This coming weekend is a four day one which is actually a disaster because it means I can’t work during it.

Writing out what I actually have to do makes it sound fully achievable, but it will take longer than I think it will. The GUI took all of yesterday. If I spend part of every day programming and part of every day practising, I should get there. Hopefully.

I haven’t bought my train tickets yet, but I really don’t want to drop out.

I’ve got 2 weeks.

Collaborative Live Coding via Jitsi Meet for Linux Users

Jitsi Meet works best in Chromium, so these instructions are for that browser. It also assumes that your live coding language uses Jack Audio.

Jack and Pulse

The first thing you need to do is to get Pulse Audio and Jack Audio running at the same time and talking to each other. For me, I was able to solve this in Qjackctl. In settings, under the option tab, go to Execute Script after startup. Paste in “pactl load-module module-jack-sink channels=2; pactl load-module module-jack-source channels=2; pacmd set-default-sink jack_out” without the quotes.

You can test if both are running at once by starting jack and then playing audio from a normal system program like your web browser. If you hear sounds, it worked.

More information about getting both running is here.

Jack Audio – Pulse Sink

Make Connections

You get two sinks. One of them is going to be used to send audio into Jitsi and the other will be used to get audio out.

Jack with two Pulse sinks and the system in/out

Start your live coding language audio server. (Ie Boot SuperCollider). Go back to Qjackctl. Click on connections. Go to the Audio tab. Make a connection from your live coding language output to Pulse Audio Jack Source-01 input. Do this by clicking on the language in the left column and the Source-01 in the right column so both are highlighted. Then click the “Connect” button on the lower left.

Disconnect the the system output from that Source’s input if you want to turn off your microphone. Do this by clicking on the system in the left column and Source-01 in the right column and clicking the “Disconnect” button.

Everything connected correctly

Chromium Settings

(These will also work for Chrome.)

First open your Jitsi Meet connection. If you are using the server at Meet.jit.si, you can skip this step.

For most other Jitsi servers, in Chromium, go to chrome://settings/content/microphone Change the mic input to Pulse Audio Jack Source-01.

Chromium Settings

Jitsi Settings

As we’re live coding, you’ll want to share your screens. Mouse over the screen so you can see the icons at the bottom appear. The one in the lower left corner looks like a screen. Click on it.

The farthest left is the screen

It lets you pick a video source. If you’re on Wayland, like most linux users have been for years now, you can share your entire screen, but you should be able to share a single window. If you don’t see your live coding language listed as a window, make sure Chromium and it are on the same virtual desktop.

Share Your Screen

Click the screen icon again to switch back to your webcam.

Fancy New Options

If you’re on a shiny new version of jitsi, such as the one at Meet.jit.si, You’ll see little carrots by the mic and video icons in the centre bottom of your browser window.

New Features!!

These allow you to pick your audio source without having to go into Chrom/ium settings. If you have more than one webcam, you can also pick which one you want to use there, without having to go into Chrom/ium settings for that either.

Be Careful of Levels!

Jitsi was made assuming that more or less one person would be talking at a time, so multiple streams at full volume can distort. Make sure to leave your output low enough to leave room for your collaborators. Your system volume controls will not work, so be sure to set the levels in your live coding language IDE.

Also be aware that while the compression sounds good for free improvisation on acoustic instruments, the transformations on digital audio will seem more pronounced. Go with it. This is your aesthetic now.

The SynthDefs for my Christmas EP

As threatened, I have once again made some Christmas music.

If you enjoy (or hate it, or are indifferent), please consider donating to the UKLGIG. cafdonate.cafonline.org/111#/DonationDetails They support LGBTQI+ people through the asylum and immigration process. Their vision is a world where there is equality, dignity, respect and safety for all people in the expression of their sexual or gender identity.

Or, if you are in the US, please donate to the National Center for Transgender Equality secure2.convio.net/ncftge/site/Donation2;jsessionid=00000000.app268b?df_id=1480&mfc_pref=T&1480.donation=form1&NONCE_TOKEN=C5EA18E62F736227261DC4CE5C50ADBE

The notes in the 5 movements all come from the same pop song, but in 4 of the movements, they pass through a class I (accidentally) wrote called MidiMangler. It’s undocumented, but the constructor expects the kind of midi events that come from SimpleMIDIFile in wslib and the .p method spits out a pbind.

The instruments are some of the sample I used a couple of years ago, but the organ is new. It’s based on one from http://sccode.org/1-5as but modified to be played with a PmonoArtic.

SynthDef(\organ, {| freq = 440, gate=1, amp=0.25, pan=0 |
    // from http://sccode.org/1-5as
    var lagdur, env, saw, panner;

    lagdur = 0.4;

    saw = VarSaw.ar(Lag.kr(freq-440)+440,
        width:LFNoise2.kr(1).range(0.2, 0.8) *
        SinOsc.kr(5, Rand(0.0, 1.0)).range(0.7,0.8));

    env = EnvGen.kr(Env.asr(Rand(0.5, 0.7), 1, Rand(1.0, 2.0), Rand(-10.0, -5.0)), gate, doneAction:2);

    amp = Lag.ar((amp / 4) * (Lag.ar(LFClipNoise.ar(lagdur.reciprocal, 0.1), lagdur) + 1)); // tremolo

    panner = Pan2.ar(saw, Lag.kr(pan,1), env * amp);

    Out.ar(0, panner);
}).add;

The other instruments are the default synthdef *cough*, a Risset bell and Karplus Strong – taken directly from a help file with no changes. These are presented at the bottom for the sake of completion. The other sound is a bomb sample I found on freesound.

The video is taken from an atom bomb test video, but slowed down and stretched. I used ffmpeg to do this. The original film was 24 frames per second. I used a ffmpeg filter to create a lot of extra in-between frames and then, separately, changed the frame rate to be much slower. The original film was a bit over 20 seconds and got stretched out to 15 minutes. The really low frame rate is a bit choppy, but I think more tweening would have just increased distortion. The commands for that were:

% ffmpeg -i trees-bomb.mp4 -filter:v "minterpolate='fps=180'" 180trees.mkv
% ffmpeg -i 180trees.mkv -filter:v "setpts=33.4*PTS" strch180.mk

The other day, I read someone putting for the idea that apocalyptic thinking is so profoundly unhelpful as to be self-indulgent. Climate change is not going out with a bang, but a very prolonged whimper, whilst, for the duration, failing to make any significant changes. We can address it and avoid many of the worst impacts, but we need to get very serious about it immediately. If we can build thousands of expensive, terrifying bombs just in case there might be a war nobody wants, surely, we can afford to spend some of that resource averting a disaster that we know is actually coming.

SynthDef(\bell, // a church bell (by Risset, described in Dodge 1997)
    {arg freq=440, amp=0.1, dur=4.0, out=0, pan;
        var env, partials, addPartial, son, sust, delay;

        freq = freq * 2;
        sust = 4;
        amp = amp/11;
        partials = Array.new(9);
        delay = Rand(0, 0.001);

        //bell = SinOsc(freq);

        addPartial = { |amplitude, rel_duration, rel_freq, detune, pan=0|
            partials.add((
                Pan2.ar(
                    FSinOsc.ar(freq*rel_freq+detune, Rand(0, 2pi), amp * amplitude* (1 + Rand(-0.01, 0.01))), pan)
                * EnvGen.kr(
                    Env.perc(0.01, sust*rel_duration* (1 + Rand(-0.01, 0.01)), 1, -4).delay(delay), doneAction: 0))
            ).tanh /2
        };

        //addPartial.(1, 1, 0.24, 0, Rand(-0.7, 0.7));
        addPartial.(1, 1, 0.95, 0, Rand(-0.7, 0.7));
        addPartial.(0.67, 0.9, 0.64, 1, Rand(-0.7, 0.7));
        addPartial.(1, 0.65, 1.23, 1, Rand(-0.7, 0.7));
        addPartial.(1.8, 0.55, 2, 0, 0); // root
        addPartial.(2.67, 0.325, 2.91, 1, Rand(-0.7, 0.7));
        addPartial.(1.67, 0.35, 3.96, 1, Rand(-0.7, 0.7));
        addPartial.(1.46, 0.25, 5.12, 1, Rand(-0.7, 0.7));
        addPartial.(1.33, 0.2, 6.37, 1, Rand(-0.7, 0.7));

        son = Mix(partials).tanh;
        son = DelayC.ar(son, 0.06, Rand(0, 0.02));
        EnvGen.kr(Env.perc(0.01, sust * 1.01), doneAction:2);

        Out.ar(out, son);
}).add;
SynthDef("plucking", {arg amp = 0.1, freq = 440, decay = 5, coef = 0.1, pan=0;

    var env, snd, panner, verb;

    freq = freq + Rand(-10.0, 10.0);
    env = EnvGen.kr(Env.linen(0, decay, 0).delay(Rand(0, 0.001)), doneAction: 2);
    snd = Pluck.ar(
        in: WhiteNoise.ar(amp),
        trig: Impulse.kr(0),

        maxdelaytime: 0.1,
        delaytime: freq.reciprocal,
        decaytime: decay,
        coef: coef);

    //verb = FreeVerb.ar(snd);
    panner = Pan2.ar(snd, pan);
    Out.ar(0, panner);
}).add;


Source code for Christmawave – overlap, duration and repetition

This is the fourth part of a series of posts about how I created my album Christmaswave. Previously, part 1 posted a list of questions and answered the first two of them: ‘What sample am I going to play?’ and ‘How many times am I going to divide it in half?’. Part 2 answered the question, ‘Once it’s chopped into little (or not-so-little) pieces, which one of them am I going to play?’. Part 3 talked endlessly in the meandering way of hangovers about playback rates.

One thing I have not addressed is how I picked which parts of source material to use. Unless the words were compelling in some way, I tended to go for phrases that were instrumental. In some songs, this left me only the intro and the outro. This is why most of the pieces have source material taken from multiple versions of the same song.

How much should an event overlap whatever comes after?

Normally, you would do this by setting the \legato part of the event, which is ‘The ratio of the synth’s duration to the event’s duration.’ I set this to 1.1 in most of the pieces, which helped make up a bit in case the slicing was in slightly the wrong place.

Most I varied:


\legato, Pwhite(0.8, 1.5)

Some depended on the duration of the it of sample I’m playing. This is what I did with Sledge Trudge


\legato, Pfunc({|evt|
var dur, legato;
dur = evt[\dur];
legato = 1;
(dur < 0.01).if({ legato = 2}, { (dur < 0.07). if({ legato = 1.5}, {legato = 1}) }); legato })

How long should I wait before going to the next thing (which might be a repetition of what I just did)?

This is a question as to what to put for the \dur part of the event, which depends on the number of frames of sample that we're playing, the sample rate of it, and the playback rate.

I pulled a lot of my source material from youtube - by using a browser plugin to download and convert to mp4 and the using audacity to convert to wav files. These files were often 48k, which is the standard for film, but audio is generally at 44.1k, so I did have to take the source file's sample rate into account.

It makes sense to calculate the start frame and duration together. This example is from Out in the Cold:


[\startFrame, \dur], Pfunc({|evt|
var buf, startFrame, dur, div, start, frames;
start = evt[\start];
div = evt[\div];
buf = evt[\buf];
frames = buf.numFrames;
startFrame= frames * (start/div);
rate =evt[\rate];
dur = (frames / buf.sampleRate) / rate * div.reciprocal;

[startFrame, dur]
})

How many times should I repeat this thing?

The glitchy repeating of the same event multiple times is a repetition of the entire event, not just some parts of it. I did this with Pclutch, which has a slightly weird syntax.


Pclutch(
pattern,
connected
).play

The pattern is just your Pbind or similar, but the connected part is slightly odd. If it's true, the Pbind is evaluated to produce a new value. It's it's false, the previous event is repeated. It's possible to use a pattern to control this.

This is the pattern I used for Walking in a Winter No Man's Land. 0 is equivalent to false and 1 is equivalent to true.


Pseq([0, 0, 0, 0, 1,
Prand([
Pseq([Pn(0,2), 1],1),
Pseq([Pn(0, 3),1],1),
Pseq([Pn(0,4), 1], 1)
],100)
])

Starting with the Pseq means that the Pclutch will repeat 4 times, then make a new event. After that, it picks randomly from 3 Pseqs. The first repeats twice, the second 3 times and the third 4 times. It will randomly pick between these repetitions for 100 times and then stop.